Computer Graphics and Visualization • Publications

In Proceedings of Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture

Approximating Logarithmic Spirals by Quarter Circles

Ulrich Reitebuch, Martin Skrodzki, and Konrad Polthier

Snapshots of the reparametrization of an approximate “better golden spiral” to an approximation of the golden spiral. The point 𝐹 is a fixpoint of the reparametrization. ¨In the last image, the angle parameter is squeezed by a factor of 1 2 and thus all angles are halved with respect to �

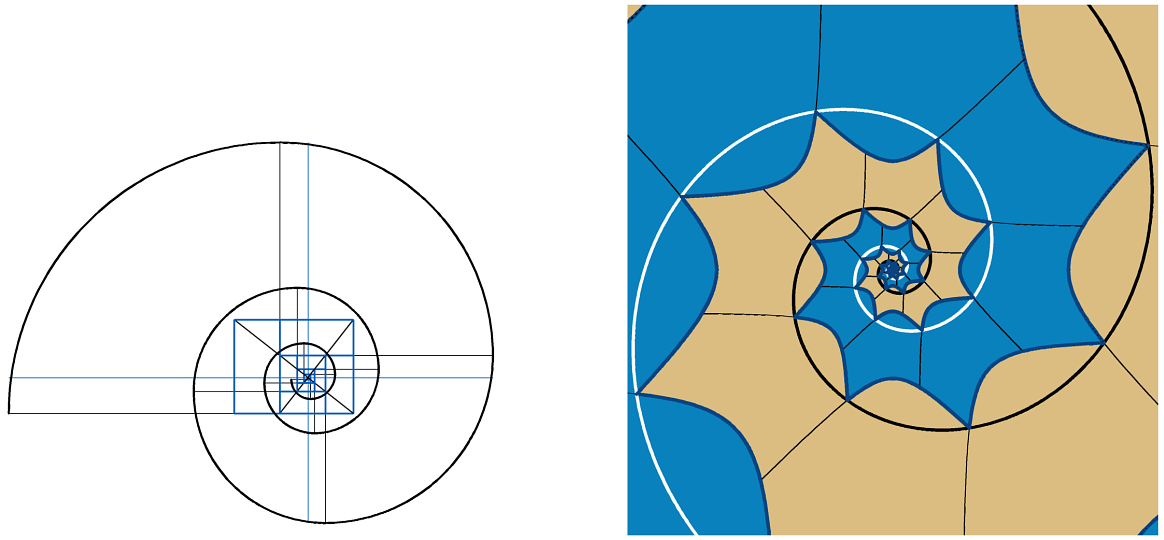
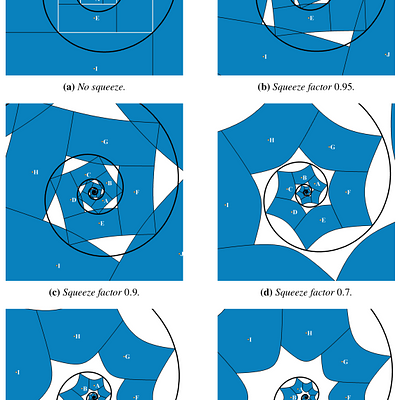
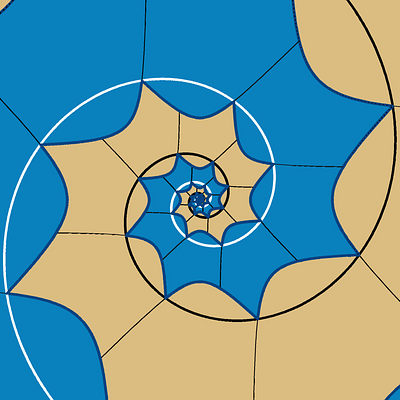
The approximation of a golden logarithmic spiral by quarter circles is well known. Starting from this, we show that any logarithmic spiral can be approximated by quarter circles in a similar way. Using our construction on a rectangle with aspect ratio √𝜙 and performing a coordinate reparametrization, we obtain an aesthetic partition of the plane as our main artwork.

More Information

Paper preprint

Citation

Ulrich Reitebuch, Martin Skrodzki, and Konrad Polthier, Approximating Logarithmic Spirals by Quarter Circles, In Proceedings of Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture, pp. 95–102, 2021.

BibTex

@inproceedings{bib:reitebuch:2021,
    author       = { Reitebuch, Ulrich and Skrodzki, Martin and Polthier, Konrad },    
    title        = { Approximating Logarithmic Spirals by Quarter Circles },
    booktitle    = { In Proceedings of Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture },
    editors      = { Swart, David and Farris, Frank and Torrence, Eve },
    year         = { 2021 },
    pages        = { 95--102 },
    publisher    = { Tessellations Publishing },
    organization  = { Bridges },
    address      = { Phoenix, Arizona },
    url          = { https://publications.graphics.tudelft.nl/papers/337 },
}