Computer Graphics and Visualization • Publications

Comput Aided Geom Des

Compressed vibration modes of elastic bodies

Christopher Brandt and Klaus Hildebrandt

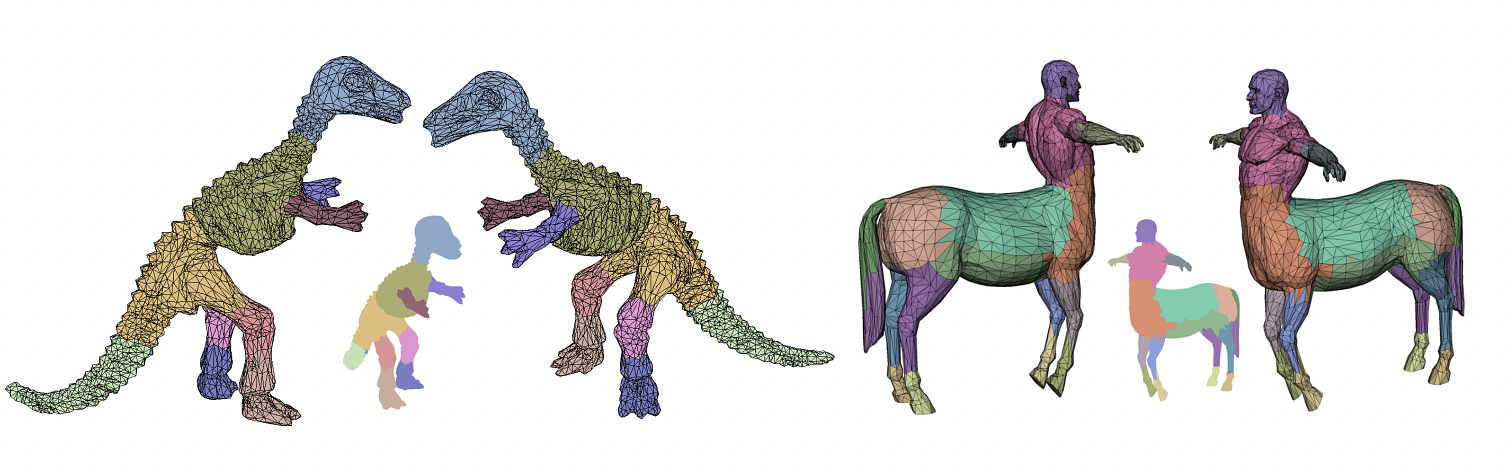
A simple segmentation scheme using our compressed vibration modes applied to the dinosaur (volumetric) and the centaur (surface) mesh

The natural vibration modes of deformable objects are a fundamental physical phenomenon. In this paper, we introduce compressed vibration modes, which, in contrast to the natural vibration modes, are localized ("sparse") deformations. The localization is achieved by augmenting the objective which has the vibration modes as minima by a L1 term. As a result the compressed modes form a compromise between localization and optimal energy efficiency of the deformations. We introduce a scheme for computing bases of compressed modes by solving sequences of convex optimization problems. Our experiments demonstrate that the resulting bases are well-suited for reduced-order shape deformation and for guiding the segmentation of objects into functional parts.

More Information

Publisher Paper preprint

Gallery

Citation

Christopher Brandt and Klaus Hildebrandt, Compressed vibration modes of elastic bodies, Comput Aided Geom Des, 52, pp. 297–312, 2017.

BibTex

@article{bib:brandt:2017,
    author       = { Brandt, Christopher and Hildebrandt, Klaus },    
    title        = { Compressed vibration modes of elastic bodies },
    journal      = { Comput Aided Geom Des },
    volume       = { 52 },
    year         = { 2017 },
    pages        = { 297--312 },
    doi          = { 10.1016/j.cagd.2017.03.004 },
    dblp         = { journals/cagd/BrandtH17 },
    url          = { https://publications.graphics.tudelft.nl/papers/143 },
}